Thermodynamique classique

Premier principe

I. Premier principe

1) Rappels sur les systèmes

On appelle système, l’ensemble des objets soumis à l’étude. On entend par objets les atomes et molécules constituant la masse du système.

ð Un système est fermé, lorsqu’il peut échanger du travail et de la chaleur avec le milieu extérieur, mais pas de matière.

ð Un système est isolé lorsqu’il n’y a aucun type s’échange avec l’extérieur.

ð Un système est ouvert lorsqu’il peut échanger travail, chaleur et matière avec le milieu extérieur.

Ces règles s’appliquent à des systèmes non radioactifs ou nucléaires. Lorsque l’on a affaires à de tels systèmes, il faut rajouter une loi de transformation de la matière en énergie.

Par convention, lorsque le système reçoit une énergie, celle-ci est comptée positive, lorsqu’il cède de l’énergie, elle est comptée négative. C’est la convention du banquier ou orientée système.

La description du système ne peut intervenir qu’après avoir établi le type du système. On établit alors les paramètres descriptifs. Ces paramètres doivent représenter les propriétés physiques étudiées et permettre de suivre leur évolution.

On distingue quatre paramètres descriptifs utilisables : la masse m qui représentent les objets du système, la pression P, le volume V et la température T.

Dans la plupart des cas, la masse n’est pas directement prise en considération, en effet on travaille souvent sur des systèmes isolés ou fermés. La masse interviendra pour normaliser les résultats afin d’en déduire des lois de comportements. Ces paramètres se séparent en deux types : Les paramètres extensifs, qui dépendent de la population et sont additifs (m et V) ; et les paramètres intensifs qui n’en dépendent pas et représentent une moyenne (P et T).

On suivra également les échanges d’énergie mécanique dW et d’énergie calorifique. Lorsqu'on a une collection d’objets, le calcul du travail élémentaire de chaque objet est infaisable, il faut donc remplacer, la force et le déplacement, qui sont des variables locales, par la pression et le volume, qui sont des variables globales, commune à tout le système.

L’énergie thermique est la grandeur associée à la chaleur perçue. La notion de chaleur est délicate comme la température, car si on voit un déplacement, la sensation physique de chaleur correspond à une perte d’énergie. Notre système biologique de contrôle de la température est basé sur la fuite thermique.

L’énergie thermique est égale à la capacité calorifique du système que multiplie la température. La capacité calorifique traduit l’admittance à la chaleur. Suivant le type de liaison chimique existant dans le solide, la capacité de transmettre la chaleur varie.

2) Enoncé, énergie interne U

a) Définition

La variation de l’énergie interne est égale à la somme de la variation de l’énergie mécanique et de la variation de l’énergie calorifique subies par le système.

Le premier principe correspond au bilan d’un système isolé dans lequel le système étudié est une partie de ce système, l’autre partie étant le réservoir.

On appelle réservoir, tout système pour lequel les échanges d’énergies et de matière sont non mesurables (variations trop faibles, non appréciables) expérimentalement.

Ce principe est valable pour des éléments stables, c’est à dire non radioactifs, sinon il faudra rajouter une équation de conversion masse – énergie, et pour des systèmes non relativistes.

Expression mathématique :

La deuxième égalité n’est valable que si l’on considère uniquement le travail des forces de pression.

b) Implications mathématiques et physiques

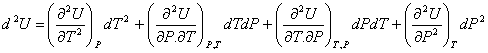
Si U est une fonction d’état, alors la variation est indépendante du chemin suivi et donc de l’ordre dans lequel on parcourt les variables. La variation ne dépend que de l’état final et de l’état initial.

Egalité des dérivées croisées :

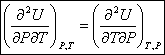
3) Fonction enthalpie H

a) Introduction de H

Cette fonction a été formellement introduite à partir de :

En effet si on choisit un chemin réversible isobare, alors le long de ce chemin on a :

Car pour une transformation réversible :

On en déduit :

En étudiant l’équation aux dimensions à pression constante (isobare) lorsque le gaz se détend sous l’action d’une quantité de chaleur Q, l’énergie reçue sert à élever la température de la mole de gaz.

Il existe donc une fonction d’état H telle que :

dont la variation à pression constante est :

Lorsque la variation est réversible.

b) Utilisation de H

La condition de réversibilité est à P = cte :

La mesure de dH à P = cte est dQ.

A volume constant :

Conclusion :

ð La mesure de la variation de U à volume constant est égale à la quantité de chaleur échangée à volume constant.

ð Par analogie avec le travail des forces de pression, on appellera VdP le « travail isochore ». Cependant ce n’est pas un travail récupérable, c’est un travail potentiel qui correspond à l’énergie de répulsion des molécules qui forment le système étudié. En effet on sait lorsqu’un système reçoit de l’énergie, l’espace moyen occupé par chaque molécule a tendance à augmenter. Si on maintient ce volume constant, il faudra que le gaz accumule l’énergie, d’où le terme de travail isochore.

On a donc :

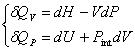
L’enthalpie étant une fonction d’état, on a l’égalité des dérivées croisées :

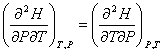
c) Capacité calorifique et chaleur spécifique

Par définition, on appelle capacité calorifique d’un système le rapport :

C’est à dire le coefficient qui lie l’élévation de température à la quantité de chaleur reçue par le système.

Il y a deux façons d’échanger la chaleur, à volume constant ou à pression constante.

et

Ces grandeurs sont mesurables. Elles représentent l’accroissement mesuré pour une quantité de chaleur connue. C’est la capacité calorifique.

Si on fait tendre la variation de température vers 0 (limite de dT).

et

Ce sont alors les chaleurs spécifiques. Elles ne sont pas mesurables. On a transformé la segmentation (discrète) en une fonction continue.

Ces grandeurs dépendent de la quantité de matière, leur unité est donc J.K ^–1.mol ^–1.

Les courbes de chaleur spécifique sont obtenues principalement à pression constante. En effet techniquement, il est plus simple de maintenir une pression qu’un volume occupé par un gaz. Les mesures en seront d’autant plus précises.

d) Relation de Mayer généralisée

Or :

Donc :

D’où

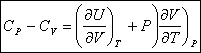
On peut l’exprimer en fonction du coefficient de dilatation thermique :

Ce qui donne :

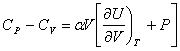
P : pression extérieure en équilibre avec le système.

Pour les gaz parfaits :

D’où :

En molaire :

C_P peut donc se déduire de C_V et vice versa. Au maximum la différence entre les deux sera égale à R, puisque le gaz parfait est un modèle, la réalité sera toujours en dessous.

De plus si l’un des deux n’est pas défini l’autre non plus.

4) Cycle de Hess

Une réaction chimique fait toujours intervenir la chaleur, soit en la consommant pour son activation, soit en la dégageant, et parfois elle peut se faire à température constante.

ð Dégage de la chaleur : La réaction est dite exothermique.

ð Consomme de la chaleur : La réaction est dite endothermique.

ð Température constante : La réaction est dite athermique.

Tout au long de cette étude, on travaillera sur un bilan, car les fonctions d’état ne dépendent que de l’état initial et final.

Ce bilan s’utilise pour prévoir les énergies mises en jeu. La puissance du cycle de Hess est basée sur le fait que l’enthalpie est fonction d’état.

L’énergie mise en jeu à pression constante correspond donc à la mesure de la variation de l’enthalpie à pression constante dans le système.

Il a donc fallu choisir un état initial servant de 0 d’origine.

ð Toutes les mesures sont ramenées à la pression constante de référence, P° = 1 bar.

ð DH° dépend de la température, il faudra donc l’indiquer.

ð On spécifiera le type de réaction en rajoutant un indice à côté du delta.

ð Le zéro des fonctions thermodynamiques à été pris tels qu’à T = 0, U = 0 et H = 0.

Pour le cycle de Hess, la référence a été faite sur les éléments de la classification périodique pris dans leur état standard à la pression de référence et à la température de 298 K. Leur enthalpie de formation est alors nulle.

Attention, pour les éléments existant sous plusieurs formes allotropiques, on en a choisi une pour référence. Par exemple pour le carbone qui peut exister sous forme graphite ou diamant, l’état standard est le carbone graphite.

Les cycles de température font intervenir les capacités calorifiques à pression constante :

Cette relation est extensive, il faudra multiplier par le nombre de mole.

On en déduit la loi de Kirchoff :

Le D_rH permet simplement de faire une première évaluation de la faisabilité de la réaction. C’est le D_rG qui permet d’affirmer qu’une réaction sera favorisée ou non par une élévation de température. De plus les lois thermodynamique ne tiennent pas compte de l’énergie d’activation, mais elle existe.

II. Second principe, entropie

La fonction entropie va permettre d’étudier l’évolution des systèmes. Elle a été conceptualisée à partir de la machine à vapeur notamment dans le cycle de Carnot. Le cycle de Carnot est un cycle théoriquement parfait parcouru par un gaz parfait de façon réversible entre deux isothermes et deux adiabatiques. Ce cycle a donné lieu à deux énoncés :

ð Clausius : Le passage de la chaleur d’un corps froid à un corps chaud n’a jamais lieu spontanément ou n’a jamais lieu sans compensation.

ð Kelvin : A l’aide d’un système qui décrit un cycle et en contact avec une source de chaleur unique, il est impossible de récupérer du travail.

Le cycle de Carnot ou une combinaison de cycles de Carnot permet de décrire n’importe quel cycle thermodynamique. On peut monter que tout cycle est décomposable en somme de cycles de Carnot. On obtient de cette façon un rendement théorique pour un cycle de :

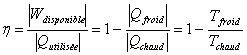
Ce rendement est toujours inférieur à 1. Toute la chaleur reçue ne pourra jamais être entièrement transformée en travail. Pour cela il faudrait que la température de la source chaude soit infinie (la matière n’existe plus) soit que la température de la source froide soit nulle (pas de chaleur à la source à basse température et dans ce cas d’après Kelvin, pas de travail).

Le rendement est nul lorsqu'il y a égalité des températures.

On introduit alors la fonction entropie :

Comme les échanges thermiques ne sont pas tous réversibles, on a :

dS représente l’échange d’entropie avec le milieu extérieur, pas celle du système étudié.

et

La fonction entropie S étant une fonction d’état, le calcul de sa variation se fera sur un chemin thermodynamiquement réversible (hypothétique ou non).

Comparons la variation d’entropie entre un chemin réversible (1) et un chemin irréversible (2) entre un état B et un état A.

Sur le chemin irréversible (2), le travail mis en jeu est W_AB².

Sur le chemin réversible (1), le travail mis en jeu est W_AB¹.

On a :

et

L’échange thermodynamique correspondant nous donnera :

et

Le calcul de la variation d’entropie se fait sur le chemin réversible et donne :

avec

Comme ce chemin est parcouru de manière réversible :

Si le trajet de B vers A est effectué par une source, i.e. par un système qui donne de la chaleur au milieu extérieur, le milieu extérieur recevra une quantité d’entropie plus grande si l’échange est réversible que si l’échange est irréversible.

Lors d’un échange spontané, la quantité ou la variation de la fonction entropie de l’échange est inférieur à la variation de la fonction entropie de la source.

Si l’on veut rendre à la source, selon un procédé irréversible ou spontané, l’entropie reçue lors du premier échange, ce sera impossible, on ne lui rendra qu’une quantité inférieure.

L’entropie d’un système isolé qui évolue spontanément augmente en fonction du temps.

1) Calcul de la variation d’entropie d’un système

Lorsque H et U sont discontinue, on est en présence d’un changement d’état. La continuité de ces fonctions est assurée en ajoutant leur valeur pendant la transition (D_transitionH).

On dit qu’un changement d’état est réversible lorsque l’on observe un équilibre entre les phases. Si le changement d’état est irréversible, on construira un chemin réversible hypothétique qui permettra de calculer exactement la variation d’entropie à la température et à la pression observées.

Le calcul de la variation d’entropie conduit au principe de Nernst (troisième principe de la thermodynamique). Pour intégrer dT / T, dT / T doit être fini, donc T ¹ 0. Et à T = 0, on fixe.

La courbe C_p en fonction de T présente des discontinuités d’ordre 1 (discontinuité infinie) et d’ordre 2 (discontinuité finie). L’allure générale est une sigmoïde.

A température nulle, la tangente à la courbe est horizontale.

Au point d’inflexion, on définit la température de Debye q_D du solide. Cette température marque la limite jusqu’à laquelle une représentation du solide par un ensemble d’oscillateurs harmoniques est valable.

A basse température [0 – 15 K], on a.

Sur la courbe, quelque soit le corps étudié, on peut répertorier au moins trois accidents :

ð A la liquéfaction (discontinuité du premier ordre)

ð A la vaporisation (discontinuité du premier ordre)

ð Quelques accidents de second ordre pour le solide.

Ces discontinuités ne sont pas ponctuelles, il y a toujours des phénomènes pré et post transitionnel.

A partir du second principe, on crée deux nouvelles fonctions d’état :

Ces fonctions permettent de comptabiliser l’énergie disponible entre l’énergie reçue et l’énergie fixée par l’entropie. En effet le terme TS représente l’énergie utilisée par l’ordre.

2) Critère d’évolution spontanée

Lorsqu’un système échange une quantité de chaleur dq avec le milieu extérieur (dq ne peut que quitter le système car on a une évolution spontanée). On distingue deux cas, soit une évolution réversible soit irréversible.

Donc :

A volume constant :

Or :

L’échange se fait à température constante :

avec

A pression constante :

avec

Seules les variations de l’enthalpie libre et de l’énergie libre peuvent être prises comme critère d’évolution spontanée. Ces fonctions s’utilisent donc en évaluant la différence de la fonction thermodynamique entre l’état final et l’état initial.

3) Quelques relations générales

a) Produit de dérivées

Equation d’état :

Fonction thermodynamiques :

, ,

On obtient des équations identiques avec P(T,V) et T(P,V).

L’équation d’état peut aussi s’écrire :

Donc :

A volume constant on a :

et

A pression constante :

A température constante :

On a donc :

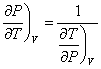
Et :

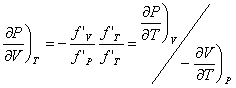
b) Transformée de Legendre

Ceci sur des chemins réversibles, c’est pour cela que l’on utilise dQ.

La plus pratique expérimentalement est l’enthalpie libre.

et

Egalité des dérivées croisées :

c) Application expérimentale

Donc en compression (dP > 0), dQ < 0, et en détente (dP < 0), dQ > 0.

L’étude de ces transformations permet d’avoir le a volumique.

Si on mesure a en faisant varier la température, on pourra suivre un changement d’état par discontinuité de a.

Pour cela, on utilise un calorimètre à flux, utilisant la différence de température générée sur des thermocouples pour produire un signal électrique fonction de cette différence.

4) Application à un corps pur dépendant de deux variables

a) Coefficients calorimétriques

Equation d’état :

Un état se définit par la connaissance de deux variables

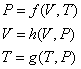
On a toujours le travail élémentaire du aux forces de pression uniquement :

Or :

Alors :

On exprime ici le travail élémentaire en fonction d’un accroissement par rapport à la pression et à la température. On peut transposer à la chaleur et obtenir trois expressions :

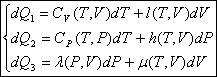
La chaleur est un élément différentiel.

En effet, la chaleur et le travail dépendent du chemin suivi or les mathématiques utilisent les différentielles totales exactes.

Que manque-t-il pour que ces éléments soient des DTE.

Montrons que les trois expressions de la chaleur sont équivalentes, pour cela, il faut qu’elles soient égales à un second ordre près.

Soit un chemin AB. On définit deux étapes intermédiaires. AC, une isobare et CB une isochore, AD une isochore et DB une isobare.

On peut donc faire ACB ou ADB soit d’abord l’isobare puis l’isochore ou d’abord l’isochore puis l’isobare.

Si les deux quantités élémentaires échangées sont équivalentes, alors le terme de différence sera du second ordre donc négligeable.

Expérimentalement ce second ordre est négligeable. De plus ce résultat est vrai quel que soit le chemin thermodynamique suivi, la pression et le volume état des variables d’états. On fait de même pour les deux autres expressions de la chaleur.

C_V : coefficient calorimétrique à volume constant.

l_T = l : coefficient de chaleur de détente isotherme.

C_P : capacité calorifique à pression constante.

h_T = h : coefficient de chaleur de compression isotherme.

l_V : coefficient de chaleur de compression isochore.

m_P : coefficient de chaleur de détente isobare.

Ces coefficients ne sont pas des constantes, ils dépendent de deux variables indépendantes.

b) Relations entre les coefficients

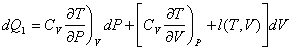
Par identification :

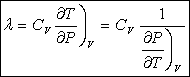et

On fait de même avec Q₂.

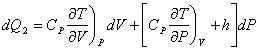
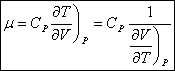et

D’où par soustraction :

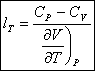et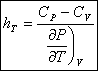

Comme nous possédons l’équation d’état du fluide, on pourra calculer les dérivées partielles intervenant. Il suffit donc de connaître C_P et C_V.

Une autre méthode pour exprimer l et h fait intervenir les fonctions U et H.

On a :

et

Condition de réversibilité :

Or U et S sont des fonctions d’état donc des DTE, leurs dérivées secondes croisées sont donc égales.

(1)

(2)

D’où :

pour un GP : l = P.

Dérivons cette dernière expression par rapport à T :

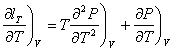
On reporte dans la première équation :

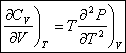
Ces expressions sont en accord avec la loi expérimentale de Joule

On procède de même pour obtenir h_T en partant des expressions du travail et de dV dans le travail. On obtient une expression de dU et de dS, puis on calcule les dérivées croisées.

et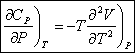

5) Détente de Joule - Thomson

La détente de Joule – Thomson est une transformation isenthalpique. C’est Hirn en 1865 qui fit des mesures précises montrant que les gaz réels ont tendance à se refroidir lors d’une détente, cela a conduit à la première approximation des gaz réels par l’équation de Van Der Waals puis par le développement du Viriel.

a) Expérience : détente isenthalpique

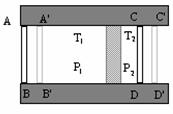Schéma du montage :

La paroi centrale est poreuse et toutes les parois son adiabatiques.

A l’état initial : le gaz occupe le volume ABCD

A t + dt : Le nouveau volume occupé est A’B’C’D’

Au cours du temps dt, la paroi AB s’est déplacée et le volume balayé est V₁(ABB’A’) et V₂(CDC’D’) de l’autre côté.

On a donc les travaux :

et

On appelle alors U₁, U₀ et U₂ les énergies internes des sous systèmes ABA’B’, ABCD et CDC’D’. On peut alors écrire :

Donc :

b) Température d’inversion

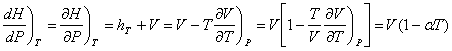
De plus :

car la transformation est isenthalpique.

D’où :

Suivant la valeur de aT, dP sera de même signe ou contraire de la variation de température. Pour le gaz parfait aT = 1, donc dT = 0. La loi de Joule est respectée : le calcul n’est pas défini.

ð aT > 1 : Accroissement de la pression avec la température. (même signe)

ð aT = 1 : Température d’inversion.

ð aT < 1 : Croissance de la pression quand la température décroît. (signe contraire)

La température d’inversion sert pour liquéfier les gaz. On comprime le gaz, puis on le détend jusqu’à l’apparition d’une goutte liquide. Cette goutte est recueillie puis on recommence.

III. Le potentiel chimique et enthalpie libre

1) Définitions

On considère la fonction G, enthalpie libre. Exprimée en fonction de T et P.

De plus :

Donc :

et

a) Variation avec la température

On obtient aussi la relation de Gibbs – Helmoltz :

, donc

Expression de la dérivée de G / T par rapport à T à P = cte.

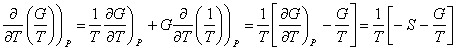
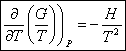
Cette relation est valable sur une différence entre un état final et un état initial. On obtient alors la relation de Van’t Hoff.

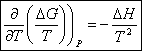
Attention, c’est D_rH pour la stœchiométrie de la réaction.

b) Variation en fonction de la pression, T = cte

Dans le cas des solides et de liquides à température constante, G varie très peu sur une plage de pression car le volume dépend peu de ce paramètre.

Pour un gaz parfait, la relation précédente devient :

Où G° est l’enthalpie libre dans l’état standard à la pression standard P°. De plus si n = 1 alors on a l’enthalpie libre molaire G_m(P).

On définit le potentiel chimique comme étant la propriété molaire de la fonction d’état correspondante.

La fonction enthalpie libre étant extensive (dépend de la quantité de matière).

Cette relation n’est valable que pour un gaz parfait. La transcription aux gaz réels se fait grâce à la notion de fugacité en prenant comme fugacité de référence la fugacité à 1 bar.

c) Approximation des gaz réels et fugacité

Pour un gaz parfait :

Alors :

Lorsque P₁ tend vers 0, f₁ tend vers P₁.

De plus :

Pour les gaz réels, on posera le facteur de compression Z :

Donc :

On peut dire que les gaz réels se comportent sous la pression atmosphérique comme des gaz parfaits. On prendra donc comme fugacité de référence f° = P°.

On prendra pour les autres fugacités, une fonction linéaire :

f = gP

Donc :

On peut donc écrire que :

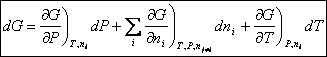
On a toujours :

et

Seulement, V et S dépendent maintenant de la composition.

A température et pression constante :

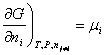, le potentiel chimique du constituant i.

Alors :

On vient d’exprimer le potentiel chimique pour la fonction enthalpie libre G. On peut le généraliser à toutes les fonctions d’état.

2) Application à l’étude des équilibres

a) Equilibre entre les phases d’un corps pur

i. Conditions d’équilibre

ð Equilibre thermique

Condition : La température est la même pour toutes les phases.

Démo : Supposons que la phase 1 soit à la température T₁, et la phase 2 à la température T₂. A volume constant, la composition à l’équilibre est connue. De plus à l’équilibre dS = 0. Soit une quantité de chaleur est transférée de la phase 1 à la phase 2, alors :

Soit :

ð Equilibre mécanique

Condition : La pression est la même pour chaque phase.

Démo :

Puisque la température est uniforme aux fluctuations près :

Or :

ð Equilibre énergétique

Condition : égalité des potentiels chimiques

Démo :

Pour la phase i :

Mais :

Donc :

Or a l’équilibre dG = 0 :

Il y a quelques exceptions notamment pour les états métastables.

ii. Variation du potentiel avec la température

Si on trace la courbe m = f(T), on observe des changements de pente à chaque changement de phase.

Quand la température augmente, le potentiel chimique diminue, car l’entropie est toujours positive. Et puisque le potentiel chimique diminue on en déduit que :

Ce qui est logique.

iii. Variation du potentiel avec la pression

Attention, dans ce cas les températures de changement de phase peuvent être différentes pour deux pressions différentes.

Le potentiel chimique augmente avec la température, car un volume est positif. Cette relation est également vraie pour des DV. Il y a quelques exceptions comme l’eau où DV < 0 pour un passage de la glace à l’eau liquide.

iv. Relation de Clapeyron

Soient deux phases, de composition n_a et n_b connues. A l’équilibre :

Le système passe à :

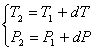
Donc :

Comme les deux phases sont toujours en équilibre :

Donc :

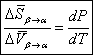
Cette relation s’applique à toutes les transformations du premier ordre.

v. Application à une fusion

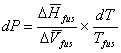
D’où :

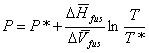
P* et T* sont les coordonnées de la fusion observée.

Si T et T* sont proches, on peut rester sous forme différentielle

vi. Vaporisation ou sublimation

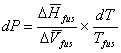
Or :

et

Or pour un gaz parfait :

Donc :

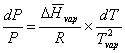
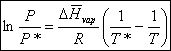
Relation de Clausius – Clapeyron.

La courbe de vaporisation s’arrête au point critique, point où le liquide et le gaz sont indiscernables. Au-delà de ce point DV_gaz®liqu = 0.

De plus autour du point triple la somme des discontinuités est nulle :

b) Règles de phases

Formule de la variance à l’équilibre :

v : variance.

C : nombre de constituants.

P : nombre de phases.

2 : nombre de paramètres indépendants (la température et la pression).

La variance représente le nombre de variables que l’on pourra modifier sans déplacer l’équilibre.

Démo :

Le nombre de variables nécessaires pour décrire un système est :

Si le système comporte C constituants, on peut alors introduire les fractions molaires pour chaque constituant et pour chaque phase et pour chaque phase, la somme des fractions molaires est égale à 1, ce qui nous donne p relations.

Le nombre de variables nécessaires et de variables indépendantes devient :

Pour un même constituant en équilibre dans les différentes phases, ses potentiels chimiques dans chaque phase sont égaux, ce qui nous donne C(P-1) relations.

Le nombre de variables indépendantes devient :

CQFD

c) Application aux équilibres chimiques

Lors d’une réaction, on a :

Or à l’équilibre :

De Plus :

D’où :

Donc :

On pose alors :

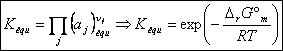
On obtient la relation de Gibbs – Helmoltz et Van’t Hoff :